CC BY 4.0 (除特别声明或转载文章外)
如果这篇博客帮助到你,可以请我喝一杯咖啡~
凸优化之运用:Lasso问题和Mnist问题的求解方法
作业一
问题描述
考虑线性测量 $ b=Ax+e$,其中 b 为 50 维的测量值,A 为 50ⅹ100 维的测量矩阵,x 为 100 维的未知稀疏向量且稀疏度为 5,e 为 50 维的测量噪声。从 b 与 A 中恢复 x 的一范数规范化 最小二乘模型如下: \(min (1/2)||Ax-b||^2_2+p||x||_1\) 其中 p 为非负的正则化参数。 在实验中,设 x 的真值中的非零元素服从均值为 0 方差为 1 的高斯分布,A 中的元素服从均 值为 0 方差为 1 的高斯分布,e 中的元素服从均值为 0 方差为 0.1 的高斯分布。
实验中,分别采用邻近点梯度下降法、交替方向乘子法、次梯度法三种方法来解决这个问题,并且之后作出相关图像分析收敛速度。
生成相关矩阵、向量的代码
import numpy as np
import matplotlib.pyplot as plt
e = np.random.normal(0,(0.1)**0.5,[50,1])
A = np.random.normal(0,1,[50,100])
x = np.zeros([100,1],np.float)
temp = np.random.normal(0,1,5)
select = np.random.randint(0,100,5)
for i in range(5):
x[select[i]] = temp[i]
b = np.dot(A,x)+e
A = np.matrix(A)
b = np.matrix(b)
e = np.matrix(e)
x = np.matrix(x)
x_optimization = x
邻近点梯度下降法
原理
邻近点梯度下降法一般适用于有一定结构但整体不可微的函数,形如 \(min f(x) = S(x) + r(x)\) 前者S(x)可微,容易求导;后者r(x)不可微,但容易求邻近点投影。问题中,$(1/2)||Ax-b||_2^2$ 可微,后者 $p||x||_1$ 的邻近点投影也易求。
邻近点投影的一种特殊形式——软门限算子:
一般形式:$x_0\in R^n,\alpha,\lambda\ \in R, x \in R^n$ \(Threadhold(\alpha,x_0) = \min_x \lambda||x||_1 + (1/2\alpha)||x-x_0||^2\) 返回的结果的一个向量$x^* \in R^n$,对于它的每一维有以下结论:$i表示第i维$ \(Threadhold(\alpha,x_0)_i = \begin{cases} x_0[i]-\lambda \alpha ,\,x_0[i]>\lambda \alpha\\\\ x_0[i]+ \lambda \alpha,\,x_0[i]<-\lambda \alpha\\\\ 0,\,else\\\\ \end{cases}\)
算法
更新步骤如下 \(x^{k+\frac{1}{2}} = x^k - step*(A^T (Ax^k-b))\\\\ x^{k+1} = Threadhold(step,x^{k+\frac{1}{2}})\\\\\)
其中step为步长,一般选取为函数的$Lipschitz \, condition(L)$相关的数,比如 \(step = \frac{1}{L} = \frac{1}{||A^TA||}\, 其中的矩阵范数任意\) 收敛条件的判定:
| 一般通过迭代次数比如1000次来控制,或者比较前后两次的x的距离大小来判定:如 $ | x^{k+1}-x^k | _2 < \epsilon$ |
实现代码
实验中,使用python编程,相关实验代码如下:
软门限算子
def thread_hold(p,alpha,x0): ##软门限算子
a = x0
t = alpha
for i in range(len(a)):
if(a[i]>p*t):
a[i] -= p*t
elif (a[i]<-p*t):
a[i] += p*t
else:
a[i] = 0.0
return a
邻近点梯度下降算法
def f(x,p): ## 目标函数
M = np.dot(A,x)-b
return 0.5*np.linalg.norm(M,ord=2)**2 + p*np.linalg.norm(x,ord=1)
def PGM_solve(err,p,x0,alpha): ## 次梯度法
ans_X = []
x_now = x0
ans_X.append(x0)
val_now = f(x_now,p)
while(True):
x_half = x_now - alpha*np.dot(A.T,np.dot(A,x_now)-b)
x_next = thread_hold(p,alpha,x_half)
ans_X.append(x_next)
err0 = np.linalg.norm(x_next-x_now)
#print("err: %.5f" % err0)
if(err0<err):
print(x_next.T)
return ans_X
x_now = x_next
运行以及绘图代码:
## 画图运行结果代码
err = 1e-5
p = 10
x0 = np.random.normal(0,1,[100,1])
alpha = 1/np.linalg.norm(np.dot(A.T,A),ord = 1)
ans_list = PGM_solve(err,p,x0,alpha)
X_dist = []
value_real = []
X_row = []
i = 0
print("the dist to the optimiztion:",np.linalg.norm(ans_list[-1]-x_optimization,ord = 2))
for x0 in ans_list:
X_dist.append(np.log(np.linalg.norm(x0-x_optimization,ord = 2)))
value_real.append(np.log(f(x0,p)))
X_row.append(i)
i += 1
plt.figure()
plt.grid(True)
plt.plot(X_row,X_dist,label = 'dist to the optimal x')
plt.ylabel('log')
plt.xlabel('times')
plt.plot(X_row,value_real,label = 'the value of f(x)')
plt.legend()
plt.show()
实验结果
实验中,对于不同的p的取值,得到以下不同的结果:
- p = 0时:
得到的$x^*$:
[[ 0.15360002 -0.61740792 0.74013353 -0.12965473 -0.45046909 0.24903346
0.66601617 -0.32888032 0.52810579 0.78278921 -0.64670267 -0.01865466
-1.36586844 -0.10236101 -0.07949768 0.60019612 -0.55438318 0.25169501
-0.45036511 0.4829098 -0.08598835 -1.01141737 0.411216 -0.54067364
-0.17471239 -1.63183869 0.11699259 1.41036064 0.01410424 0.71982976
1.11801011 -0.32234055 -0.15183024 0.06482722 -0.2796284 0.25865785
0.23978955 -0.06832938 1.49034414 0.09382201 -0.75253437 0.10436963
0.20040118 -0.49178092 -0.20770116 -0.02277012 0.94087551 -0.87960575
-0.17105014 -0.56944551 0.2439499 -0.2458873 -0.0408685 0.97049357
0.4488112 -0.65686207 -0.50223396 1.06476275 -0.05031732 0.16535196
-0.42040232 -0.40280395 -1.30676412 0.7698993 -0.04363971 0.71887193
0.51548802 -0.40013244 -0.74871417 0.2961535 0.61023001 -0.13855902
0.73223549 -0.69097947 0.99811654 -0.5466045 -0.28836318 0.30191984
-0.32751547 1.63179288 0.18225466 -0.72487191 0.38891477 -1.28350433
1.04721556 -0.2186386 -1.47935682 1.07740704 -0.57796358 0.22691212
0.12249136 0.54258727 -0.00970764 -1.46594374 0.45491053 -0.31440676
-0.12576028 -0.11186738 0.73091799 -0.34133264]]
最终最优解与原始解即给定的最优解的欧式距离: 6.685495788626413
收敛情况图:
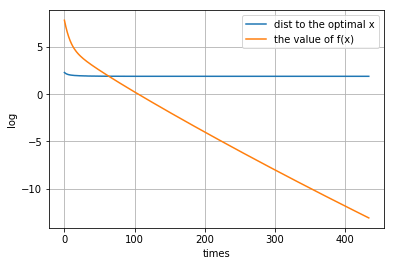
-
p = 2.4
[[ 0.07308723 0. 0. 0. 0. 0. 0. 0. 0. 0.00570265 0. 0. 0. 0. 0.01415677 0. 0. 0. 0. 0. -0.00901876 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -1.39496252 0. 0. 0. -0.00277158 0. 0. 0. -0.03061028 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -0.00298155 0. 0. -0.0024028 0. 0. 0.01425206 -0.00231333 0. 0. 0. 0. -0.04413433 0. 0. 0. 0. 0.06352649 0.01946604 0. 0. 0. 0. 0. 0.30244851 0. 0. 0. 0. 0. 0. 0. 0. -0.0127845 0. 0. 0. 0. 0. 0. -0.01677917 -0.04890622 0. 0. 0. 0. 0. 0. ]]距离原始最优解的距离: 0.16696787243346062
收敛图像:
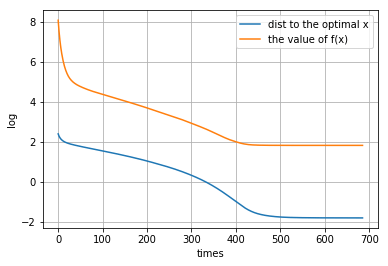
-
p = 10
得到的$x^*$
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -1.22592767 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.14564372 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]]距离原始最优解的距离: 0.3222533138802545
图像:
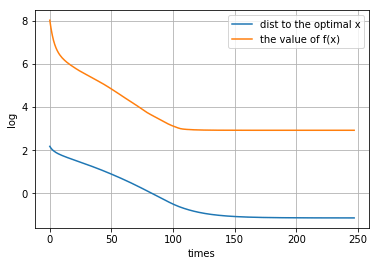
-
p = 50
得到的$x^*$
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -0.22730891 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]]距离原始最优解的距离: 1.2789445681027676
图像:
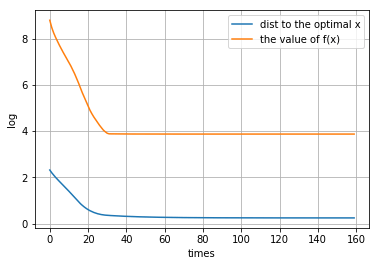
| 可见,对于不同的p值,p值越大,得到的最有解越稀疏。而且可以看到在一定范围内p值的增大,得到的实际最优解会往原始最优解靠近,但是超过一定程度,反而远离,这是$p | x | _1$ 惩罚过度造成的。其中,p取2.4时,得到的最有解与原始最优解最接近。 |
交替方向乘子法
原理
交替方向乘子法适用于一类目标函数有结构的优化问题,一般形式: \(min f_1(x) + f_2(y)\\\\ .s.t \, Ax+By = 0\)
原问题需要经过一定转换成这种形式,构造约束:$x = y$,然后原优化问题转变为:
\[min \, (1/2)||Ax-b||_2^2 + p||y||_1 \\\\ .s.t \,\, x-y = 0\\\\\]之后做拉格朗日乘子以及增广,变为求解无约束优化问题:
\[L_{\frac{1}{t}}(x,y,v) = (1/2)||Ax-b||_2^2 + p||y||_1 + (1/t)<v,x-y> + \frac{1}{2t}||x-y||_2^2\]然后使用交替乘子法法来解决这个问题,分别对x,y做下降,v做上升,本质是在求鞍点。
\[x_{k+1} = arg\min_x L_{\frac{1}{t}}(x,y_{k},v_k)\\\\ y_{k+1} = arg\min_x L_{\frac{1}{t}}(x_{k+1},y,v_k)\\\\ v_{k+1} = v_{k} + (1/t)(x_{k+1}-y_{k+1})\\\\\]算法
初始化:$x_0,y_0,z_0,k = 1,t = t_0>0$
迭代更新步骤如下: \(x_{k+1} = (A^TA + (1/t)I)^{-1}(A^Tb + (1/t)(y_k - v_k))\\\\ y_{k+1} = Threadhold(pt,x_{k+1}+v_k)\\\\ v_{k+1} = v_{k} + (1/t)(x_{k+1}-y_{k+1})\\\\ k += 1\\\\\) 其中的t是与步长和惩罚项(约束x和y之间的差异)相关的一个参数。
| 收敛条件一般设为:k的迭代次数或者前后两次迭代中向量的差的距离来判定,如:$ | x_{k+1}-x_k | _2<\epsilon$ |
实现代码
ans_X = [] # 记录x
y_k1= np.random.randint(100,200,[100,1])
x_k = y_k1
v_k1 = np.random.normal(0,1,[100,1])
t = 10 #步长的倒数
p = 20 # 惩罚项
err = 1e-5
x_size = len(y_k1)
k = 0
ans_X.append(x_k)
while(k<700):
x_old = x_k
#x,z交替下降;y上升
x_k = np.dot(np.linalg.inv(np.dot(A.T,A)+(1/t)*np.eye(x_size)),
np.dot(A.T,b)+(1/t)*(y_k1-v_k1) )
y_k1 = thread_hold(p,t,x_k+v_k1)
v_k1 = v_k1 + (1/t)*(x_k-y_k1)
ans_X.append(x_k)
#print("x: ",np.linalg.norm(x_k-x_optimization,ord = 2))
if(np.linalg.norm(x_k-x_old)<err):
break
k += 1
### 绘图代码
X_dist = []
X_real = []
X_row = []
i = 0
print(ans_X[-1].T)
print('dist to optimization: ',(np.linalg.norm(ans_X[-1]-x_optimization,ord = 2)))
for x0 in ans_X[:200]:
X_dist.append(np.log(np.linalg.norm(x0-x_optimization,ord = 2)))
X_real.append(np.log(f(x0,p)))
X_row.append(i)
i += 1
plt.figure()
plt.grid(True)
plt.plot(X_row,X_dist,label = 'dist to the optimal x')
plt.ylabel('log')
plt.plot(X_row,X_real,label = 'value of f(x)')
plt.legend()
plt.show()
实验结果
-
p = 0
[[ 39.78120771 -41.73945307 92.15011186 52.94112166 159.10213158 116.580929 29.54665622 -51.79049928 176.8298065 -85.35418459 31.62059287 96.59416052 -4.69925173 106.52464594 74.94560837 -8.2156462 158.34971607 55.61773481 196.20161866 195.38627071 163.8627529 172.66966109 198.69924899 66.5332916 83.34919108 170.720259 59.56018205 190.28692788 44.03523406 62.88703802 26.68157594 198.97473029 142.01357719 80.1608372 139.88404939 228.93033222 36.59762676 9.9157182 -107.35846169 75.33967439 145.38473123 73.29075919 27.5638663 15.09597698 6.28571716 198.6685374 155.9145629 124.25373376 -15.54179432 59.26506327 94.70605104 52.58272788 23.5706076 73.05065217 104.7918066 68.93035902 37.5191307 125.68884969 177.79629564 257.93010119 80.43495312 69.87518733 103.0513823 84.36798715 120.18603158 95.93759876 -50.62043589 77.36574021 58.46154665 146.30433322 103.33495042 111.06874181 -31.7762251 152.75969981 80.19660745 171.17303631 65.18342791 -82.39325394 55.34256931 65.03850618 130.02805052 131.38663951 111.94326154 -40.55874826 83.59612532 -38.59313571 65.10990013 6.14993443 18.92666546 161.12368656 81.95552907 167.77525985 88.58936339 -1.77145375 -29.49691655 218.66118553 159.08870855 22.07562514 53.47123042 77.89073382]]距离原始最优解的距离: 1108.1589574271613
图像:
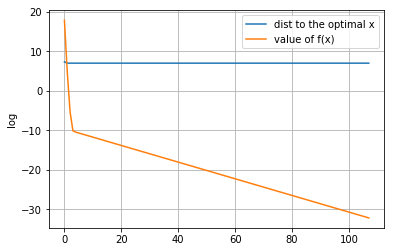
-
p = 2.4
[[ 5.48458841e-02 -7.30842017e-03 4.60103378e-03 -8.00545748e-02 5.58513686e-02 5.17316441e-02 1.56106021e+00 -2.72915700e-02 -6.10263066e-02 4.90339030e-03 1.61473291e-01 -1.93030109e-02 3.22147190e-02 -2.49513621e-02 -2.69488648e-02 -5.08504900e-02 6.46440084e-02 2.59681660e-02 8.51664652e-02 3.10286167e-02 -5.22654444e-02 -5.76447612e-02 -1.62976375e-01 9.31156146e-02 -1.00679103e-01 1.42461949e-02 4.63749422e-02 -3.30427946e-02 -1.51575083e-02 2.02525522e-02 -2.32974205e-02 7.67771536e-02 2.41772169e-03 -2.24385398e-02 6.59883736e-02 2.76560188e-02 -5.77693207e-02 -7.37002559e-03 1.94506559e-02 1.61225894e-02 -6.61226441e-03 -4.16106567e-02 4.44751721e-02 -7.64736784e-02 1.07584073e-01 2.20913646e-02 -7.52149226e-03 -5.25178062e-02 1.77963965e-01 9.08152589e-03 6.63043059e-02 -1.93971831e-02 3.68274018e-03 -7.60554207e-03 1.20387148e-02 1.46908834e-02 -1.71612124e-02 -1.04862064e-01 3.99911236e-05 2.37584077e-02 5.37459362e-02 -6.83796351e-02 1.64708338e-02 9.23938188e-03 9.28486686e-03 -7.38587049e-04 -4.27390377e-02 -7.36788506e-02 -1.57728673e-02 1.75892411e-02 5.51427214e-02 3.58443143e-02 4.45599441e-02 2.50540765e-02 -4.80022261e-02 -8.07623190e-02 3.32844472e-02 -5.35906564e-04 7.36148521e-02 5.66951291e-02 1.03409468e-02 -6.54930177e-03 -4.22341734e-02 -1.46595151e-03 -1.82943854e-02 -5.67586303e-02 -5.64020220e-02 4.46813681e-02 3.55167413e-02 9.09106963e-03 3.98864618e-02 -6.46593890e-02 -1.45685352e-03 3.47667370e-02 2.34002550e-02 8.24886557e-03 -3.49077503e-02 2.31145277e-02 9.46576296e-02 8.21547792e-02]]距离原始最优解的距离: 0.6717995628241801
图像:
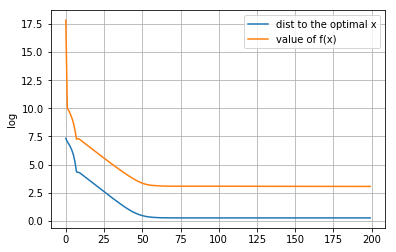
-
p = 10
[[ 0.10210642 -0.06696867 0.0624416 -0.14620859 0.0292154 0.01876656 0.74666996 -0.01088196 -0.06167612 0.02345605 0.22541563 0.11915275 -0.00962796 0.15048497 0.01562492 -0.0132576 0.12488901 0.00594928 0.13157922 0.13322615 -0.0977552 0.03213019 -0.18969016 0.08162859 -0.1057494 -0.00860091 0.09572657 0.01503606 -0.07165664 0.04829767 -0.02394151 -0.00385449 -0.06735231 -0.09589053 0.0139595 0.10770025 0.00366294 -0.11820322 0.09837472 0.03036061 0.04258437 -0.15104426 0.02086572 -0.07221288 0.18339119 0.02210569 0.02584092 0.06720841 0.16366334 0.03257969 -0.00211557 0.0562243 0.05412666 -0.15594019 -0.01830741 -0.01873569 0.03614208 -0.13131782 -0.11898256 -0.08035107 0.09600567 -0.02207468 -0.08758486 0.02929714 -0.05297732 0.03322114 0.01363021 -0.1282267 -0.14106505 -0.05009227 0.06162378 0.145767 0.09838268 -0.09477182 -0.07029744 -0.13916854 0.02886737 -0.05010044 0.03242331 0.00691476 -0.05883528 0.10972375 -0.13878561 0.01072714 0.08525212 -0.02787977 -0.09169074 0.04528336 0.13757055 0.09531995 0.05806893 -0.0877117 0.05854332 -0.01644144 0.24709922 0.0836163 -0.02904153 0.05615176 -0.01449597 0.08284158]]距离原始最优解的距离: 1.308548233559688
图像:
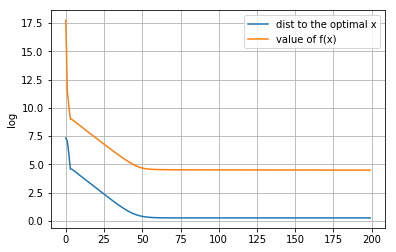
-
p = 50
[[ 0.0976437 -0.06139018 0.0689107 -0.14769098 0.03362325 0.02795482 0.75129067 -0.00511661 -0.07072429 0.02368501 0.23241807 0.12112894 -0.00657701 0.15181625 0.02325206 -0.00971197 0.1223728 0.00870661 0.13040686 0.12728482 -0.09639158 0.03675164 -0.18821597 0.08421068 -0.10753269 -0.00405823 0.10100954 0.01048893 -0.0690546 0.05353072 -0.02149028 -0.00394141 -0.06893041 -0.09181005 0.01071293 0.09999582 0.00260686 -0.11490674 0.09245365 0.02511346 0.04996776 -0.15581265 0.02000074 -0.06476883 0.18371082 0.02259777 0.02440123 0.06876834 0.16046976 0.02475548 -0.00196577 0.05201795 0.05844888 -0.15195422 -0.01965658 -0.011991 0.04511834 -0.12570215 -0.11795666 -0.09218123 0.10249598 -0.01807127 -0.08384084 0.03643547 -0.05930377 0.03464453 0.01126174 -0.12736659 -0.14543666 -0.0438376 0.06899083 0.1489796 0.09686128 -0.09684398 -0.06834795 -0.14105062 0.02967089 -0.05656195 0.03848964 0.01096054 -0.05827271 0.10762348 -0.13641183 0.0093104 0.099758 -0.01944275 -0.09169481 0.04377104 0.13300929 0.08817508 0.0636986 -0.09073315 0.05969707 -0.01114743 0.25210313 0.07373965 -0.02795383 0.05742787 -0.01495086 0.07750093]]距离原始最优解的距离: 1.306944061229278
图像:
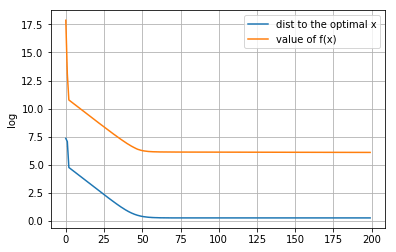
次梯度法
原理
次梯度法实际上是普通梯度下降法的一个变种,由于目标函数在某些地方不可微,故原来的梯度用次梯度来代替。
在本问题中目标函数不妨记为$f(x): R^n \rightarrow R$,它的次梯度为一个$R^n$的列向量,i表示第i个元素 \(f'(x)_i = (A^TA(x-b))[i] + \begin{cases} p,\, x[i]>0\\\\ -p,x[i]<0\\\\ 任选[-p,p]中的值,\,else \end{cases}\)
算法
每次迭代更新: \(x_{k+1} = x_{k} - \alpha f'(x_k)\) 其中,$\alpha$为步长,一般来说,次梯度法要保证收敛需要使用递减步长,实验中使用了不可加平方也不可加的步长序列即: \(\alpha_k = \alpha_0*\frac{1}{\sqrt{k}},k>0,\alpha_0 = \frac{1}{||A^TA||}\)
实现代码
获取次梯度代码:
def gradient(x1,p,alpha):
a = x1 - alpha*A.T*(A*x1-b)
for i in range(len(x1)):
if(np.abs(a[i])<1e-5):
a[i] = 0.0
elif(x1[i]>0):
a[i] -= p*alpha
elif(x1[i]<0):
a[i] += p*alpha
return a
次梯度下降算法:
def Solve(x0,p,err,alpha0):
x_now = x0
k = 1
alpha = alpha0
ansList = []
while(k<1000):
x = gradient(x_now,p,alpha)
#print(x)
ansList.append(x)
now_value = temp
x_now = x
k += 1
alpha = k**(-0.5)*alpha0
return ansList
程序主体代码:
x0 = np.random.normal(0,1,[100,1])
err = 1e-5
p = 50
X_point = []
#print(x)
alpha0 = 1/np.linalg.norm(np.dot(A.T,A),ord = 2)
ans_X = Solve(x0,p,err,alpha0)
### 绘图代码
X_dist = []
X_real = []
X_row = []
i = 0
print(ans_X[-1].T)
print('dist to optimization: ',(np.linalg.norm(ans_X[-1]-x_optimization,ord = 2)))
for x0 in ans_X[:200]:
X_dist.append(np.log(np.linalg.norm(x0-x_optimization,ord = 2)))
X_real.append(np.log(f(x0,p)))
X_row.append(i)
i += 1
plt.figure()
plt.grid(True)
plt.plot(X_row,X_dist,label = 'dist to the optimal x')
plt.ylabel('log')
plt.plot(X_row,X_real,label = 'value of f(x)')
plt.legend()
plt.show()
实验结果
-
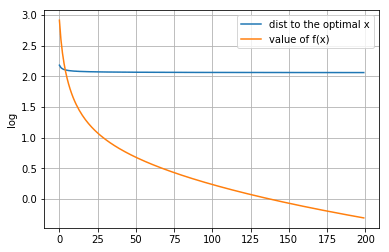
p = 0时
[[-0.31958408 0.45260367 0.0198952 0.58246096 0.49209077 0.07200605 -0.01752615 -0.84821112 0.20096714 -1.29860569 1.3069339 -0.05352533 0.96415672 -0.41797876 0.6847735 0.02672455 0.08856603 -1.34822515 -0.06089169 -0.8609725 -0.05427692 0.94253762 0.66632115 -0.47651595 0.26763409 0.51224363 -1.96871375 0.34606869 -0.09336145 0.27182639 1.07386776 0.82802153 -0.62471696 0.0027603 0.07440627 0.45072121 -1.7967477 -0.14577253 0.45056446 -0.20349565 0.12621031 -0.39663732 0.6182013 0.5822594 -0.54380408 0.73928773 -0.58774825 -0.55200926 0.55856347 -0.32429724 0.64244727 -0.10529518 -0.05125296 -0.73144392 -0.45393068 0.39725327 0.96525449 1.86445901 -0.75329854 -0.38054527 0.3641292 0.08398668 0.27660229 -0.00319436 -0.55526332 -0.48146652 -1.41194587 -0.43437068 -0.72952376 1.13262602 0.77597437 1.25922338 0.26043756 -0.0727982 -0.1906999 0.99221456 0.51971123 -0.35744617 -0.8228225 -0.06072643 -1.00805365 1.13244822 1.06943965 -1.09260201 -0.55177169 0.28082447 -0.57216744 -0.40578112 1.7966365 1.5412951 0.33139801 -0.33673179 -0.31973677 0.84634941 1.8708398 -0.51633012 1.21714374 -0.31856857 -0.25194112 0.61877854]]距离原始最优解的距离: 7.827884692879529
图像:
-
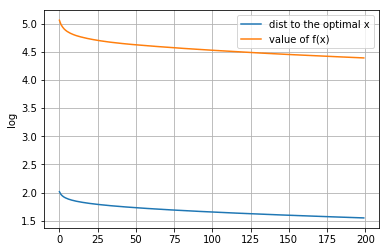
p = 2.4
[[-1.80743972e-02 3.64403982e-04 -3.15813293e-02 2.18089317e-01 -1.07837448e-04 -7.33850792e-02 1.04156043e-04 9.96713242e-03 0.00000000e+00 2.53307270e-02 -4.62172561e-05 1.00582840e+00 -2.94441545e-01 1.75464078e-01 -1.24830129e-01 -2.30936030e-01 -5.58347942e-02 5.39328681e-05 -2.61613706e-01 2.06096578e-04 -1.73343186e-05 9.48723760e-05 7.13330721e-01 4.65743783e-01 9.23065363e-04 -1.02160958e-05 4.49188328e-04 -2.06182088e-01 -1.30996840e-04 4.47016705e-01 3.27458281e-04 2.68470513e-01 -4.56758026e-05 -4.75476196e-04 -2.66271002e-03 -4.00484087e-05 -1.04397281e+00 -3.70217542e-01 -2.01595470e-01 -2.04392136e-01 9.25473900e-02 6.36846289e-01 9.22327686e-02 1.16274440e-04 1.08945479e-02 0.00000000e+00 7.67882359e-05 -2.42644727e-04 -4.75975885e-02 3.41587140e-01 8.53767493e-02 8.48805690e-05 -1.37998532e-04 -7.55031213e-01 -2.64969889e-04 3.59266343e-01 3.03921119e-01 3.65449146e-01 -1.77457131e-04 -4.95512279e-01 3.46358783e-04 1.65186781e-05 1.01571992e-01 -2.64286313e-05 -1.30850444e-04 2.88751058e-01 -3.49016338e-01 1.21243704e-04 -2.41209878e-01 2.36790680e-01 -9.30806640e-05 9.37038515e-01 7.82493662e-05 -7.74542032e-05 -1.30972794e-01 -3.13022159e-04 -5.48874375e-05 -1.72816582e-04 1.89357898e-04 -4.37527339e-03 3.98319014e-04 3.34826559e-02 -3.56654219e-01 -2.19009693e-01 2.80359015e-01 1.47432635e-01 2.40819135e-02 -2.67868375e-01 3.82795315e-01 -1.03441930e-05 -1.81002923e-01 -1.16092758e+00 3.18429781e-01 1.50493173e-01 2.52982377e-01 2.50366683e-01 9.49346050e-02 -4.28643939e-01 1.64970938e-01 -1.20093697e-04]]距离原始最优解的距离: 2.9103781686518486
图像:
-
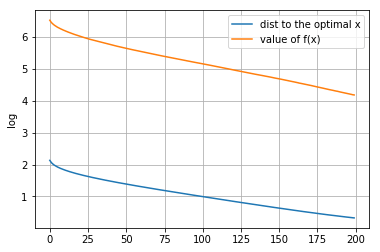
p = 10
[[ 2.19225912e-04 -4.07637574e-04 -1.83205480e-04 0.00000000e+00 4.88341853e-04 1.38643727e-03 6.62290923e-04 -7.46077906e-05 -5.56641258e-04 3.98377330e-04 -8.69294263e-04 1.58953475e-04 -1.09719243e-03 1.25924824e-03 9.79450965e-04 -9.38709058e-04 -7.47092741e-04 -5.69753535e-04 -5.45923041e-04 -1.78935420e-04 1.32331641e-04 -7.71548852e-04 -3.21195083e-04 8.79048092e-01 -4.77706901e-04 -4.58358834e-05 2.95722188e-04 5.22615415e-04 -1.07823244e-03 1.20771218e-03 1.05424365e-03 6.52011553e-04 -3.95187346e-04 -4.96531621e-04 -3.76750342e-05 -7.36394926e-04 -8.61964571e-04 -3.74799199e-04 4.02605025e-04 8.86144855e-04 -1.69436098e-04 -4.71701431e-04 3.17721202e-04 1.59931210e-04 -1.01203405e-04 -1.46715364e-03 2.23866422e-04 -1.00700920e-03 -6.84477038e-04 7.12259471e-04 7.00228062e-04 -1.17378295e-03 4.17467271e-04 -1.40920708e+00 6.68822682e-04 4.43777374e-04 -6.47158755e-04 0.00000000e+00 -3.44008845e-04 1.63565593e-03 4.34786740e-04 3.57126923e-04 1.22455755e-04 8.76347023e-04 -1.20787722e-03 4.71650169e-04 -1.04629695e-03 -1.47176248e-03 -4.03469653e-04 1.43421189e-03 -5.79722945e-04 -2.98652787e-04 -3.85626571e-04 -5.03385064e-04 -1.04172297e-03 -3.90556567e-04 -7.83572721e-05 2.85321067e-04 -5.10357985e-04 -6.14331266e-04 3.12156536e-04 9.38514493e-04 -2.93172487e-04 5.70646851e-04 2.70738331e-04 -6.13209213e-04 -1.67148854e-03 1.64775918e-03 2.71014912e-04 6.47786384e-04 -1.66998053e-04 -1.02190862e+00 -6.23227529e-04 1.35948441e-05 -7.67169802e-06 4.04207004e-04 -5.33266224e-04 -1.04453795e-04 2.51645445e-04 6.34003302e-04]]距离原始最优解的距离: 0.537495281798165
图像:
-
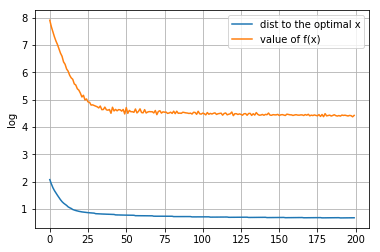
p = 50
[[-2.61875236e-03 1.84454595e-04 -3.10774848e-03 4.35566324e-04 -2.36975362e-03 5.44599650e-03 9.66344884e-04 6.53219106e-03 2.23705263e-03 3.19433127e-03 2.61203708e-03 5.06801016e-04 -6.00952652e-03 -1.79391192e-03 6.80052073e-03 -4.75523454e-03 -3.01039303e-04 2.54370636e-03 -1.28849123e-03 3.53079945e-03 -3.54627126e-03 4.15788294e-03 -1.68696865e-03 4.24115288e-03 -6.11929208e-03 -1.43516491e-03 2.63789846e-03 -3.32209404e-03 -9.71493136e-04 -3.57650856e-03 -2.67365359e-03 2.33180228e-03 5.69495051e-05 -2.87879912e-03 3.44450982e-03 3.24582478e-03 2.63101668e-03 -1.99197035e-03 -2.35979975e-03 4.08976545e-03 3.67528799e-03 2.68482706e-03 3.85144215e-03 2.93337956e-03 -5.57319483e-03 -5.70057748e-03 -3.35589423e-03 -4.30617269e-03 -3.30756931e-03 -5.54597543e-04 3.06706520e-03 -5.13310601e-03 7.00438020e-03 -4.74851992e-01 -8.25780021e-04 -2.28821567e-05 1.35881904e-03 -1.46242832e-03 2.82169264e-03 2.11798810e-03 1.90508041e-03 3.83852403e-03 -4.84252438e-03 -4.55780417e-03 -4.18747033e-03 4.21521174e-03 3.50289032e-03 -6.94198037e-03 4.18836176e-03 3.52723517e-03 5.52122357e-03 1.72086084e-03 -5.14318007e-03 1.43386791e-03 3.51149010e-04 3.93737985e-03 1.42839453e-03 4.45686034e-03 2.65276696e-03 5.36468971e-03 1.55932475e-03 -5.77509308e-04 1.15826083e-04 -3.67299040e-03 2.46585461e-03 -2.42863314e-03 -6.27670556e-03 -2.82425078e-03 -7.48191258e-03 2.05964441e-03 -6.27106815e-03 -4.50758165e-01 -6.17695389e-04 -4.77019973e-03 5.77403601e-03 -2.38814736e-03 5.65460790e-03 5.56984461e-04 6.15561443e-04 1.01503812e-03]]距离原始最优解的距离: 1.9154401144466695
图像:
总结(一)
通过运用三种梯度相关的算法解决这个问题,可以发现,不同的p值对最优解的有不同的影响。而且,注意到,对于前面邻近点梯度下降法和交替方向乘子法,p越大,得到的最优解x*越稀疏。然而,对于次梯度法,即使增大p,得到的x*也不一定稀疏;另外,次梯度法下降的时候,它的实际函数值在最优解附近会震荡,这也是与理论分析吻合的。
其次,步长的选择,在实验中是非常重要的,合适的步长才能确保收敛,才能得到不错的效果。
从三种算法算法的收敛曲线来看,邻近点梯度法和交替方向乘子法可以达到线性收敛速度,次梯度法则相对较慢,是一个次线性的收敛速度。
总之,对于同一个问题,我们可以采取不同的算法来求解它,这就要求我们要根据算法的性能,选取最合适的算法。
作业二
问题描述
使用梯度相关的下降算法来解决MNIST数据集上的Logistic Regression问题,并分析每次分类的精度。
相关原理
如何预测
首先,进行分类用到了机器学习领域非常经典的函数$softmax(x):R^T \rightarrow R^T,T一般是分类的类别数$它是可以将一个列向量x各个元素映射到(0,1)区间的函数,也就是得到了各类别的概率值。设$y = softmax(x)$,则是类别$i,i\in {0,1,…,N-1}$ 的概率为$P(i) = y[i],表示取列向量的第i个元素$。
对于一个给定的样本$X_0 \in R^n$,给一个参数矩阵 $ W \in R^{T*N} $,那么预测该样本的类别:
\[i = f(x) = arg \max_i(softmax(W*X_0)[i]),R^N \rightarrow R\]即取 $ R^T $ 向量概率最大的下标。
要求解什么
根据上面的预测原理,不难发现,W的值是关键。目标就是得到一个$W^*$,使得它的预测最准确。我们要使用梯度下降法来求解,就需要定义与W相关的损失函数。
损失函数
首先,从单独一个样本来考虑如何来定义它的损失函数。假设一个样本$X_0 \in R^n$,标签值为$y_0$,那么我们肯定希望经过我们的预测函数$f(X_0)$后返回值就是$y_0$,也就是说经过$softmax()$后第$y_0$ 维的值最大,换句话说,就是使得$softmax()$的第$y_0$维尽量大。也就是说极大化$softmax(W*X_0)[y_0]$.
注以下解释采用极大似然估计的角度来解释这个损失函数,另外有从信息论交叉熵的角度解释。 对于k个样本构成的样本集合$X: {X_0,X_1,…,X_k}$,假设它们相互独立,那么使得所有这些样本都尽可能正确的概率应该为:$P(W) = \prod_{i=0}^ksoftmax(W*X_i)[y_i]$
我们想办法极大化它,那么可以取对数,并记为:
$J(W) = \sum_{i=0}^k log(softmax(W*X_i))[y_i]$
一般我们优化问题中是极小化目标函数,所以添加一个负号,得到最终的损失函数: \(J(W) = -\sum_{i=0}^k J_i(W,X_i,y_i) = -\sum_{i=0}^k log(softmax(W*X_i))[y_i]\) $J_i(W,X_i,y_i)表示每一个单独样本的损失函数$。
梯度的求解
这个函数,难点在于求它的梯度,我们可以分别求解每个样本的梯度,然后相加。网上^[1]^的推导,得出以下结论: \(\nabla W[i][j] = (softmax(W*X)[i]-\delta_{ij})X[i]\\\\ 其中:\delta_{ij} = \begin{cases} 1,i =j\\\\ 0, i \not= j \end{cases}\)
算法
解决这个问题,不难发现这是一个关于W的凸函数,于是采用梯度下降法(BGD)和批量随机梯度下降法(MSGD)来求解W。其中,如果在MSGD中取batchsize等于整个数据集的大小,那么SGD就退化为BGD了,所以下面介绍MSGD算法。
假设样本总大小为data_size。基本思路为:先选定batchsize,即每一批样本的大小,然后把样本拆分成data_size/batchsize这么多份,然后每次随机其中一批样本,然后对选中的样本进行梯度下降,即损失函数变为: \(J(W) = -\frac{1}{batchsize}\sum_{i=m_0}^{m_0+batchsize}J_i(W,X_i,y_i)\) 每次梯度下降得到的W,然后在测试集上测试其正确率。
终止条件为迭代次数:设为1000次左右。
实现代码
该问题中 $ W \in R^{10(748+1)},X_i \in R^{748+1} $ .原本做法是有一个 ** 偏置 $ b\in R^{10} $ **,即 $ WX+b $ ,所以直接把W加上一列,相应的样本X也在最后添加1。这样做,可以在形式上少一个参数。
实验中的数据集均从Mnist官网^[2]^ 直接下载得到。
导入数据集的代码
import numpy as np
import matplotlib.pyplot as plt
data_path = 'D:\\notebook_python\\Mnist_datebase\\'
#data_path = "/Mnist_datebase/mnist_test.csv"
Test_set = np.loadtxt(data_path + 'mnist_test.csv',delimiter=',')
Data_set = np.loadtxt(data_path + 'mnist_train.csv', delimiter= ',')
data_size = len(Test_set[0])-1
stablesoftmax的定义
def softmax(x):
exps = np.exp(x)
return exps / np.sum(exps)
def stablesoftmax(x):
"""Compute the softmax of vector x in a numerically stable way."""
shiftx = x - np.max(x)
exps = np.exp(shiftx)
return exps / np.sum(exps)
获取梯度的代码:
def Gradient(W,x,y): #姑且定义W为 10*785的矩阵
N = 785
x1 = np.dot(W,x)
a = stablesoftmax(x1)
W2 = np.zeros([10,N],np.float)
for i in range(10):
for j in range(N):
if(int(y) == i):
W2[i][j] = (a[i][0]-1)*x[j][0]
else:
W2[i][j] = a[i][0]*x[j][0]
return W2
获取预测的类别的代码:
def argmaxP(a):
ans = -np.inf
site = 0
for i in range(len(a)):
if(ans<a[i][0]):
ans = a[i][0]
site = i
return ans,site
对一份样本做一次梯度下降的代码:
#BGD,全局梯度下降
def BGD_Solve(Data_set,W0,alpha):
W_old = W0
for i in range(len(Data_set)):
y = Data_set[i][0]
x = Data_set[i][1:]
x = np.append(x,1)
x = x[:,None]
W = Gradient(W0,x,y)
W_old -= alpha*W
return W_old
测试正确率的代码:
def Test_err(Test_data,W):
err_cout = 0
for x in range(len(Test_data)):
x1 = Test_data[x][1:]
x1 = np.append(x1,1)
x1 = x1[:,None]
y1 = Test_data[x][0]
y_preidct = argmaxP(stablesoftmax(np.dot(W,x1)))[1]
#print("y_predict: ",y_preidct,"y1: ",y1)
if(y_preidct != int(y1)):
err_cout += 1
return err_cout/len(Test_data)
执行主体代码:最后使用了递减步长。
iteration_K = 100
W0 = np.zeros([10,785],np.float)
batch_size = 800
data_size = len(Data_set)
i = 0
W1 = W0
alpha0 = 0.007/(data_size/batch_size)
alpha = alpha0
ans_correct = []
ans_times = []
k = 0
while(k<iteration_K):
W1 = BGD_Solve(Data_set[i:i+batch_size],W1,alpha)
i = np.random.randint(0,(data_size//batch_size)-1)*batch_size # 随机
#print("i: ",i)
err = Test_err(Test_set,W1)
ans_correct.append(1-err)
ans_times.append(k)
#print("correct:",1-err)
if(k>15):
alpha = alpha0/k
k += 1
plt.figure()
plt.grid()
plt.plot(ans_times,ans_correct)
plt.xlabel('times')
plt.ylabel('correct rate %')
plt.plot(ans_times,ans_correct1,'r',label = 'correct rate')
plt.legend()
plt.show()
实验结果
对于不同的batchsize,迭代次数为100,得到了以下结果:
-
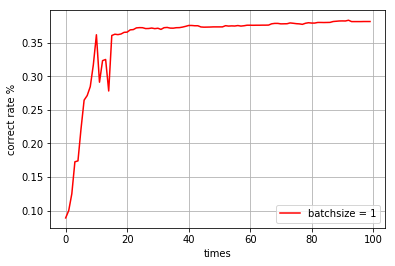
batchsize = 1,迭代100次
time cost: 38.88164 s
correct rate: 0.38149999999999995
-
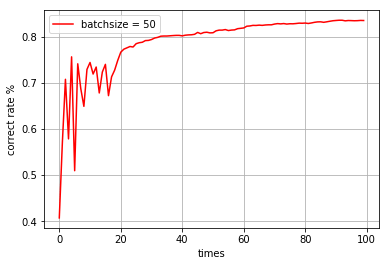
batchsize = 50,迭代100次
time cost: 104.87715 s correct rate: 0.835
-
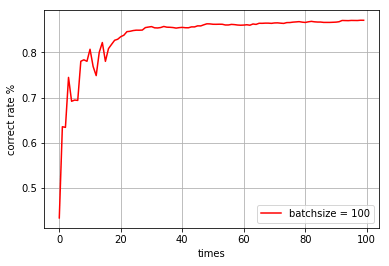
batchsize = 100,迭代100次
time cost: 124.97161 s correct rate: 0.8712
-
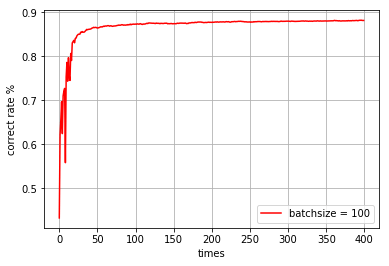
batchsize = 400,迭代100次
time cost: 522.98277 s correct rate: 0.8815
-
batchsize = 800,迭代100次
correct rate: 0.9072
图像:
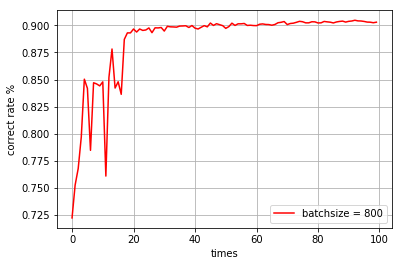
总结(二)
实验中,主要难点在于这个过程损失函数的理解以及它梯度的求解。 这一次Mnist数据处理的实验中,采用不同batchsize的MSGD算法来求解参数W,可以看到,不同的batchsize大小会影响算法运行的时间和识别的正确率。一般来说,batchsize不宜太小,太小的话,正确率不高;太大的话,时间花费太大,速度不行。实验发现,batchsize一般超过100至1000可以在时间和正确率上得到一个不错的平衡。 另外,可以注意到,随机梯度法,它的收敛曲线也是震荡的,于是可以考虑后面使用递减步长也减小这种震荡。
参考资料
[1] softmax导数的推导:https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/, 2019-6-8
[2] Mnist官网:http://yann.lecun.com/exdb/mnist/, 2019-6-4
