CC BY 4.0 (除特别声明或转载文章外)
如果这篇博客帮助到你,可以请我喝一杯咖啡~
题目
23. Merge k Sorted Lists
Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.
Example:
Input:
[
1->4->5,
1->3->4,
2->6
]
Output: 1->1->2->3->4->4->5->6
解法
我使用的解法便是使用堆来做。思路大概就是维护一个ListNode*小顶堆,然后每次取出堆顶的元素,插入到结果链表中,并把堆顶元素的 *next 进入堆中。时间复杂度为 $O(kn \times log k)$, 空间复杂度为$O(kn \times logk)$.
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
struct CMP{
bool operator()(const ListNode* a, const ListNode* b){
return a->val >= b->val;
}
};
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
if(lists.size() == 0) return nullptr;
priority_queue<ListNode*,vector<ListNode*>,CMP> q;
for(int i=0;i<lists.size();i++){
if(lists[i])
q.push(lists[i]);
}
ListNode* cur = new ListNode(-1);
ListNode* head = cur;
while(!q.empty()){
ListNode* p = q.top();
q.pop();
ListNode* now = new ListNode(p->val);
cur->next = now;
cur = cur->next;
if(p->next) q.push(p->next);
}
ListNode* p = head->next;
delete head;
return p;
}
};
看了官方解答后,有一种分治的思想,值得学习。该方法采用了归并排序里使用的分治的思想来解决。下面图片也是来自官方解答:
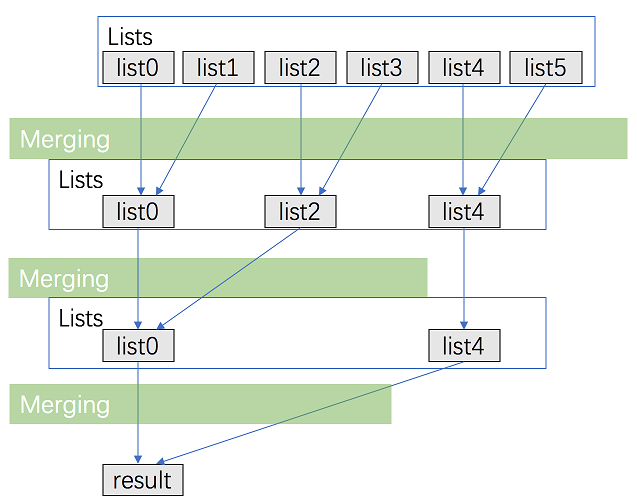
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
//官方解答这里写得确实不错
if ((!a) || (!b)) return a ? a : b;
//官方解答这里写得确实不错
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) { //官方解答这里写得确实不错
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
//官方解答这里写得确实不错
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* merge(vector <ListNode*> &lists, int l, int r) {
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
};
于此,解决这类题的思路又多了一种了!
